EVM Deep Dives: The Path to Shadowy Super Coder 🥷 💻 - Part 3
Demystifying Storage Slot Packing - Key Knowledge for the EVM Hackers
This is the third installment in the “EVM Deep Dives” series, this article will build on the knowledge gained from Part 1 & Part 2 so if you haven’t read these yet I encourage you to do so.
In this episode, we’ll dig into how contract storage works, provide some mental models to aid your understanding and deep dive into storage slot packing. If the term “slot packing” is foreign to you don’t worry, knowledge of slot packing is vital for EVM hackers and you’ll have a deep understanding of it by the end of the article.
If you’ve ever attempted the Ethernaut Solidity Wargame Series or other Solidity “Capture The Flag” type games you’ll know slot packing knowledge is often the key to cracking the puzzles/hacks.
Storage Fundamentals
A high-level overview of storage fundamentals has been done brilliantly in this “Program the Blockchain” post. I’ll provide a refresher of the key points required for this article however I highly recommend reading their full article.
Data Structure
We’ll start with the data structure of contract storage, this provides us a solid foundation upon which the rest of our knowledge will sit.
Contract storage is simply a key to value mapping. It maps a 32-byte key to a 32-byte value. Given our key is 32 bytes in size we can have a maximum of (2^256)-1 keys.
32 bytes is equal to 256 bits which gives us (2^256)-1 binary numbers to choose from for the key.
All values are initialised as 0 and zeros are not explicitly stored. This makes sense since 2^256 is approximately the number of atoms in the known, observable universe.
No computer can hold that much data. This is also the reason setting a storage value to zero refunds you some gas as that key value no longer needs to be stored by the nodes on the network.
Conceptually storage can be viewed as an astronomically large array. Our first key with binary value 0 represents item 0 in the array, the key with binary value 1 represents item 1 in the array etc.
Fixed Size Variables
Contract variables that are declared as storage variables can be split into 2 camps fixed-size and dynamic-size. We’re going to focus on fixed-size variables and how the EVM can pack multiple variables into a single 32-byte storage slot.
To learn more about dynamic size variables refer to the “Program the Blockchain” post.
Now that we know storage is a key-value mapping, the next question is how are the keys assigned to the variables. Say we have the following solidity code.
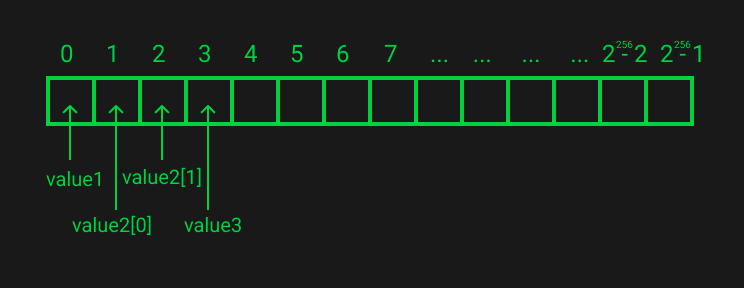
Given all these variables are fixed size the EVM can use reserved storage locations (keys) starting from slot 0 (key of binary value 0) and moving linearly forward to slot 1, 2 etc.
It will do this based on the order the variables are declared in the contract. The first declared storage variable will be stored at slot 0.
In this example slot 0 will hold variable “value1”, variable “value2” is a fixed-sized array of 2 so will take up slots 1 & 2 and finally, slot 3 will hold variable “value3”. The diagram below shows this.
Now let’s take a look at a similar contract and inspect how the variables are stored in this scenario.
You might expect this to take up slots 0 to 3 as in the previous example. We had 4 values to store in our previous example (taking into consideration the array of size 2) and we have 4 values to store in this example.
You may be surprised to hear that in this example only storage slot 0 is used. The key difference is the unit types that are used for the variables.
Before all variables were of type uint256 which represents 32 bytes of data. Here we use uint32, uint64 & uint128 which represent 4, 8 and 16 bytes of data respectively.
Slot Packing
This is where the term slot packing arises. The solidity compiler knows it can store 32 bytes of data at a storage slot. As a result, when “uint32 value1”, which only takes up 4 bytes, is stored at slot 0 when the next variable is read in the compiler will see if it can be packed into the current storage slot.
Given slot 0 had 32 bytes of space and value1 only took up 4 of them as long as the next variable is less than 28 bytes in size it will also be packed into slot 0.
For the above example we start with 32 bytes at slot 0;
value1 is stored at slot 0 which takes up 4 bytes
slot 0 has 28 bytes remaining
value2 is 4 bytes which is <= 28 therefore it can be stored at slot 0
slot 0 has 24 bytes remaining
value3 is 8 bytes which is <= 24 therefore it can be stored at slot 0
slot 0 has 16 bytes remaining
value4 is 16 bytes which is <= 16 therefore it can be stored at slot 0
slot 0 has 0 bytes remaining
Note that uint8 is the smallest solidity type, therefore packing cannot be smaller than 1 byte (8 bits)
The image below shows how the 32 bytes of data in slot 0 hold all 4 variables.
EVM Storage Opcodes
Now we understand the data structure of storage and the concept of slot packing let’s take a quick look at the 2 storage opcodes SSTORE & SLOAD.
SSTORE
We’ll start with SSTORE it takes in a 32-byte key and a 32-byte value from the call stack and stores that 32-byte value at that 32-byte key location. Check out this EVM playground to see how it works.
SLOAD
Next, we have SLOAD which takes in a 32-byte key from the call stack and pushes the 32-byte value stored at that 32-byte key location onto the call stack. Check out this EVM playground to see how it works.
The question you should be asking yourself at this stage is if SSTORE and SLOAD only deal in 32-byte values how can you extract a variable that has been packed into a 32-byte slot.
If you take our example above when we run SLOAD on slot 0 we’re going to get the full 32-byte value stored at that location.
This value will include the data for value1, value2, value3 & value4. How does the EVM extract the specific bytes in that 32-byte slot to return the value that we need?
The same goes for when we run SSTORE if we’re storing 32 bytes every time how does the EVM ensure when we store value2 it doesn’t overwrite value1. When we store value3 it doesn’t overwrite value2 etc.
These are the questions we’ll look to answer next.
Storing & Retrieving Packed Variables
Below is a simple contract that imitates the example we looked at above. The only addition is a store function that sets the variable values and has to read one variable to perform some arithmetic.
The store() function in the above solidity will perform the exact operations we had questions about.
Storing multiple variables in a single slot without overwriting existing data and retrieving a variable’s specific bytes from a 32-byte slot.
Let’s start by looking at the end state of slot 0 and work backward from there. Below is both the binary and hexadecimal representation of slot 0.
Remember that hexadecimal numbers are ultimately seen as binary numbers by the machine. This is important as a number of bitwise operations are used in slot packing.
Note the values you can see in the hexadecimal, 0x115c which is equal to 4444 in decimal, 0x14d = 333, 0x16 = 22 & 0x01 = 1. These correspond to what we see in our solidity code. One slot holds 32 bytes of data which is 64 hexadecimal characters or 256 bits.
Bitwise Operations
Slot packing makes use of 3 bitwise operations, AND, OR & NOT. These correspond to 3 EVM opcodes with the same naming. Let’s take a quick look at each one.
AND
Below we have two 8 bit binary numbers. In an AND operation the 1st bit in the first number is compared with the 1st bit in the second number.
If both values are a 1 then the AND statement returns true and the first bit of our result will equal 1 otherwise the statement returns false and the bit will equal 0.
This continues ie the 2nd bit of our first number is compared with the 2nd bit of our second number etc.
OR
In the OR operation, only one of the values needs to have a value of 1 for the statement to return true. Using the same inputs as above we get a completely different output.
NOT
NOT is slightly different in that it only takes in one value rather than performing a comparison on 2 . NOT performs logical negation on each bit. Bits that are 0 become 1, and those that are 1 become 0.
Let’s now jump into how these are used in the above solidity example
Slot Manipulation - Slot Packing SSTORE
We’re going to focus on solidity line 18.
value2 = 22;At this stage some data, value1, has been stored in slot 0, we now need to pack some additional data into the same slot.
All the logic we see for this example is the same as when value3 & value4 are stored. We’ll look at how this is done conceptually and an EVM playground will be provided for you to explore further.
We start with the following values.
Note “0xffffffff” is equal to “11111111111111111111111111111111” in binary.
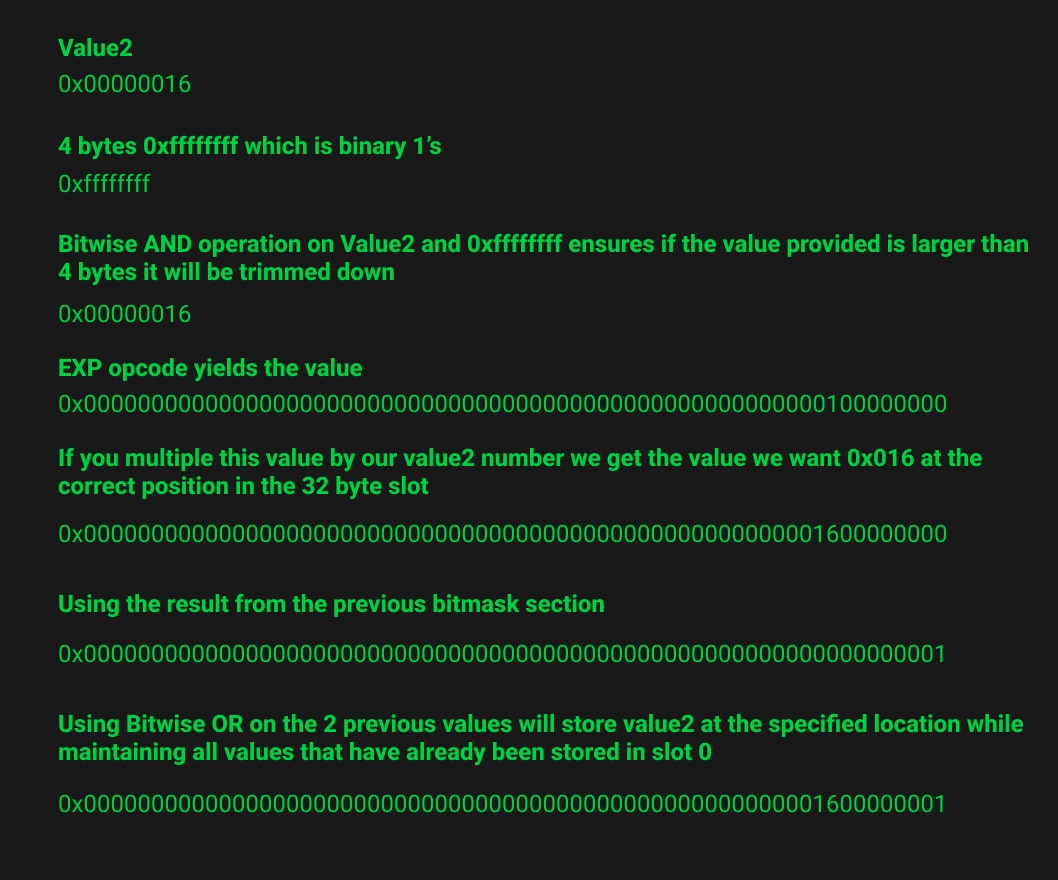
The first thing the EVM does is use the EXP opcode which takes in a base integer and an exponent and returns the value.
Here we use 0x0100 as the base integer which represents a 1-byte offset and raise it to exponent 0x04 which is the start position for “value2”. The image below shows why the returned value is useful.
We can see that the result of the EXP function enables us to insert our data 0x16 at the correct position (4-byte offset).
We can’t use this value however as it would overwrite value1 which has already been stored. This is where bitmasks are utilised.
The above image shows how a bitmask can be utilised to get all data from a slot except for the bytes you are looking to overwrite. In this case, value2’s bytes were already set to 0 however if they had not been we would have seen this data wiped.
Here’s another example to crystalise what is happening. This is the same process but looking at what would happen if all 4 values had already been stored and we wanted to update value2 from 22 to 99. Look out for the existing 0x016 value being zeroed out.
You may already be thinking about how a bitwise OR could help us combine the values we have. The image below shows the next steps.
We can now use SSTORE on this 32-byte value at slot 0 which contains the data for both value1 & value2 at the correct byte positions.
Slot Manipulation - Retrieving a Packed Variable SLOAD
For retrieval, we will focus on solidity line 22.
uint96 value5 = value3 + uint32(666)We’re not interested in the arithmetic, we’re interested in value3 being retrieved to perform the calculation.
We have a slightly different set of starting values.
Much of what we have seen already will be reused for retrieval with some modifications.
We have retrieved value3 from our packed slot 0. Hexadecimal 0x14d is equal to 333 which is what we set in the solidity code above.
Again bitmasks and bitwise operations are used to help extract specific bytes from the 32-byte slot. This value is now on the stack and can then be used by the EVM to calculate “value3 + uint32(666)”.
EVM Playground
I’ve taken all the opcodes executed in the store() function we just explored and put them into an EVM playground. Here you’ll be able to interactively play with the opcodes that are used and see how the call stack and contract storage change as you jump through them.
I’ve left comments next to the opcodes on the 2 sections we explored (solidity lines 18 & 22). I highly encourage you to check it out and jump through the opcodes it will greatly enhance your understanding.
Check it out here.
You should now have an in-depth understanding of how storage slot packing works and how the EVM is able to retrieve and store bytes in specific locations in a 32-byte slot.
Although the EVM opcodes SLOAD & SSTORE only deal in 32-byte chunks we can use bitwise operations and bitmasks to store and load the data we want.
In Part 4 of the series, we take a look under the hood of the Go Ethereum (Geth) client to see how it implements the SSTORE & SLOAD opcodes.
Hope you enjoyed the article.
noxx
Twitter @noxx3xxon




















i wonder why the prefer EXP & DIV instead of SHIFT ops.
Being pedantic, isnt "Given our key is 32 bytes in size we can have a maximum of (2^256)-1 keys." incorrect? As you also have the possibility of having 0 as a key.