EVM Deep Dives: The Path to Shadowy Super Coder 🥷 💻 - Part 6
A Treasure Trove of Data - Transaction Receipts & Event Logs
Navigating on-chain data is an essential skill for anyone looking to build in the Web3 space. Understanding the data structures that make up a blockchain can help you think about new and creative ways to parse that data.
Today we’re going to be deep-diving into a key data structure within the EVM, transaction receipts and their associated event logs. If you’ve coded in Solidity before you’ve likely emitted event logs yourself, they make up a huge portion of the data available to us on-chain data.
In this article, we’ll journey from the block header all the way down to the internals of an event log giving you a comprehensive understanding of what data is available to you and how it was created.
Why use Logs
Before we begin I want to briefly touch on why we use Event logs as solidity developers.
As a cheaper alternative to data storage, as long as the contract does not need access to it.
As a method to trigger web3 applications that are listening out for specific event logs.
EVM nodes are not required to keep logs forever and can remove old logs to save space. Contracts cannot access log storage so they are not required for nodes to execute a contract. Contract storage on the other hand is required for execution so cannot be removed.
Ethereum Block Merkle Roots
In Part 4 of the EVM Deep Dives, we dived into the Ethereum architecture specifically the state Merkle root. The state Merkle root was 1 of 3 Merkle roots contained in the block header. The other 2 were the transaction Merkle root and the transaction receipts Merkle root.
To frame this deep dive we’re going to reference block 15001871 on the Ethereum chain which contains 5 transactions, their associated receipts and the event logs that were emitted. This will help us link any concepts we learn back to a real-world example.
Block Header
We’ll start with the block header. There are 3 components we’re interested in, the “Transaction Root”, the “Receipt Root” and the “Logs Bloom”.

Within the Ethereum client underneath the “Transaction” and “Receipt” roots are Merkle Patricia Tries containing the transaction data & receipt data for all transactions and receipts within that block.
We won’t dive into how a Merkle Patricia Trie works. For the purpose of this article understanding that the node has access to all the transactions and receipts is all we need to know.
Let’s take a look at the real block header for block 15001871 by querying an Ethereum node.
Take note of the block header logsBloom, it is a key data structure that we will refer back to later in the article.
For now let’s start with the data that lies underneath the Transaction Root, the Transaction Trie.
Transaction Trie
The “Transaction Trie” is the data set that generates the transactionsRoot and records the transaction request vectors.
Transaction request vectors are the pieces of information required to execute a transaction.
The fields included in a transaction can be seen below.
Type = The transaction type (LegacyTxType, AccessListTxType, DynamicFeeTxType).
ChainId = The EIP155 chain ID of the transaction.
Data = The input data of the transaction
AccessList = The access list of the transaction
Gas = The gas limit of the transaction
GasPrice = The gas price of the transaction
GasTipCap = The gasTipCap per gas of the transaction
GasFeeCap = The fee cap per gas of the transaction
Value = The ether amount of the transaction
Nonce = The sender account nonce of the transaction
To = The recipient address of the transaction. For contract-creation transactions, To returns nil
RawSignatureValues = The V, R, S signature values of the transaction
Let’s take a look at some real data from a transaction within block 15001871. We’ll use the first transaction 0x311ba3a0affb00510ae3f0a36c5bcd0a48cdb23d803bbc16f128639ffb9e3e58.
Let’s use Geth’s ethclient to query a node. Note ChainId and AccessList both have “omitempty”, which means if the field is empty it will be omitted from the response.

This transaction represents a transfer of USDT to this address 0xec23e787ea25230f74a3da0f515825c1d820f47a.
The to address is the ERC20 USDT contract 0xdac17f958d2ee523a2206206994597c13d831ec7.
If we look at the input data we can see the function signature 0xa9059cbb which corresponds to transfer(address,uint256) , the address to send the USDT to 0xec23e787ea25230f74a3da0f515825c1d820f47a and the amount 0x2b279b8 = 45251000 in decimal or $45.251.
What you might notice about this transaction data structure is that it doesn’t tell us anything about the outcome of the transaction. Was the transaction successful? How much gas did it use? What event logs were emitted?
This is where transaction receipts & the “Receipt Trie” come in.
Receipts Trie
A shopping receipt records the outcome of a transaction. An object in the Receipt Trie does the same thing for an Ethereum transaction along with some additional details.
The questions posed above are what a transaction receipt looks to answer. We’re going to focus on the third question. What event logs were emitted?
Again I’ve queried the chain to get some us some real data. We’re going to look at the transaction receipt for the transaction we looked at above 0x311ba3a0affb00510ae3f0a36c5bcd0a48cdb23d803bbc16f128639ffb9e3e58.

Let’s run through the fields.
Type = The transaction type (LegacyTxType, AccessListTxType, DynamicFeeTxType).
PostState (root) = The StateRoot post-execution of the transaction. You may note it’s 0x in the query above this is likely due to EIP-98.
CumulativeGasUsed = Sum of gasUsed by this transaction and all preceding transactions in the same block.
Bloom (logsBloom) = Bloom filter for event logs (We’ll dig into this in the next section, remember we saw a logsBloom field in the block header as well)
Logs = Array of log objects
TxHash = The transaction hash that the receipt is associated with
ContractAddress = Address of the deployed contract if the transaction was a contract creation. 0x000…0 if the transaction isn’t a contract creation.
GasUsed = Gas used by this transaction
BlockHash = Hash of the block this transaction occurred in
BlockNumber = Block number for the block this transaction occurred in
TransactionIndex = Transactions index within the block. The index determines which transaction is executed first. This transaction is at the top of the block and therefore has an index 0.
Now we know what a transaction receipt is composed of we can zoom in on the logsBloom and the log array within the transaction receipt.
Event Logs
We noted in the transaction section that this transaction is a USDT transfer. I’ve grabbed a snippet of code from the USDT contract on Etherscan for us to review.
We can see the Transfer event is declared on line 86 and that 2 of the input parameters have the keyword “indexed”.
You may be wondering what the indexed keyword means. When an event input is “indexed” it enables us to do quick look-ups for a log with that input.
For example with an indexed “from” as seen above I can ask the question get me all event logs of type Transfer with a “from” address of 0x5041ed759dd4afc3a72b8192c143f72f4724081a between blocks X & Y. How this indexing works under the hood will be covered in the next section.
We can also see that this event log is emitted when the transfer function is called on line 138. Note this contract was created with an earlier solidity version hence why the emit keyword is missing.
Again let’s take a look at the real on-chain data for this transaction.

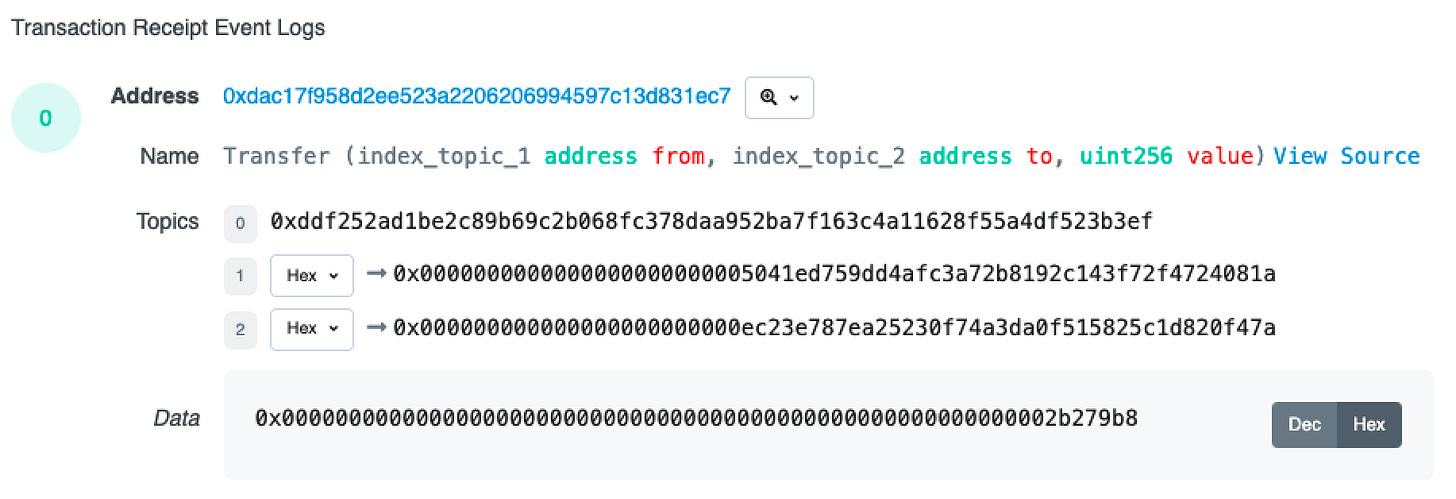
If you refer to the comments in the Log struct you’ll see descriptions for each field. The fields we want to take a closer look at are address, topics and data.
Topics
Let’s start with topics. Topics are indexed values. You’ll notice we have 3 topics in our on-chain query while the Transfer event only has 2 indexed parameters (from & to). This is because the first topic is always the hash of the event signature.
In this case the event signature is Transfer(address,address,uint256). We keccak256 hash this value to give us ddf252ad1be2c89b69c2b068fc378daa952ba7f163c4a11628f55a4df523b3ef. Try it for yourself here (Note input type is text).
This makes sense, if we look at the question we wanted to ask above we wanted to limit it to event logs of type Transfer only. There may be multiple Events that have a from field so by indexing the event signature as well we are able to filter by event type.
We can have a maximum of 4 topics and each topic is 32 bytes in size. We can declare 3 indexed parameters given the first is taken by the event signature.
There is one case when the first topic isn’t the hashed event signature. This is when we declare an anonymous Event. This opens up the possibility of having 4 indexed parameters rather than 3 but we lose the ability to index on the Event name. One other advantage of anonymous events is that they can be cheaper to deploy since they don’t force you to use 1 additional topic.
The other topics are the indexed “from” and “to” values from the Transfer Event.
If the type of an indexed parameter is larger than 32 bytes (i.e. string and bytes), the actual data isn’t stored, but rather the keccak256 digest of the data is stored.
Data
The data section contains the remaining (non-indexed) parameters in the event log. In our case this is just “value” 0x0000000000000000000000000000000000000000000000000000000002b279b8 which is equal to 45251000 in decimal or $45.251.
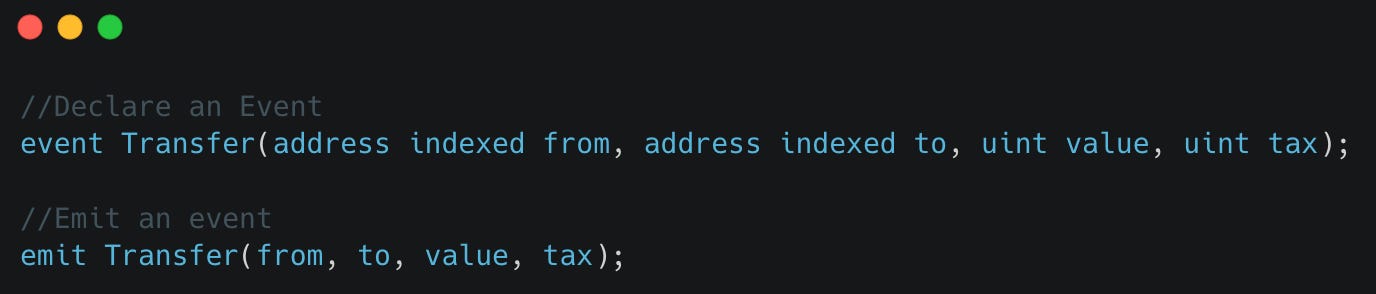
If we had more they would be appended to the data item. Let’s look at an example where there is more than 1 non-indexed parameter.
In this example, we add an additional “tax” field to the Transfer event. Let’s assume tax is 20% so our tax value should be 20% of 45251000. This is 9050200 in decimal which is 0x8a1858 in hex, the type is uint = uint256 so we’ll need to pad the hex value to 32 bytes.
The resulting data item would be 0x0000000000000000000000000000000000000000000000000000000002b279b800000000000000000000000000000000000000000000000000000000008a1858.
Address
The address field is the address of the contract that emitted the event. One important note on this field is that it will also be indexed despite it not being included in the topics section.
Again this makes sense, the Transfer event is part of the ERC20 standard meaning when we filter logs on the ERC20 Transfer event we’re going to get the transfer events from all ERC20 contracts.
By indexing the contract address we can narrow down the search to a specific contract/token that we are interested in (USDT).
Opcodes
Finally, let’s touch on the LOG opcodes of which there are 5. They go from LOG0 for when no topics are included to LOG4 when 4 topics are included.
LOG3 is what would have been used in our example. It takes in
offset = memory offset, which represents the start location of the data field input
length = length of the data to read in from memory
topic1 = value for topic1
topic2 = value for topic2
topic3 = value for topic3
Offset and length define where in memory the data is located for the data section.
Now we understand how the log is structured we can finally answer the question of what happens under the hood when a topic is indexed.
Bloom Filters
The secret to how indexed items enable faster lookup is Bloom filters.
Llimllib has a great definition of what these data structures are.
A Bloom filter is a data structure designed to tell you, rapidly and memory-efficiently, whether an element is present in a set.
The price paid for this efficiency is that a Bloom filter is a probabilistic data structure: it tells us that the element either definitely is not in the set or may be in the set.
The base data structure of a Bloom filter is a Bit Vector.
Below is an example of a small bit vector. The white cells represent bits with value 0 while the green cells represent bits with value 1.
These bits were set to 1 by taking some input and hashing it. The value of the resulting hash is used as the bit index for which bit should be updated.
The bit vector above is the result of using 2 different hash functions on the value “ethereum” to get 2 bit indexes.
The hashes represent hexadecimal numbers. To get the index we can take this number and convert it into a value between 0 and 14. There are various ways to do this such as using modulo 14.
See this great site for this example and try it out yourself.
Lookup
Ok, so we have a bloom filter for a transaction which we now understand to be a bit vector. For Ethereum, the inputs that are hashed to determine which bits to update in the bit vector are the address field and the topics of the event log.
Let’s refer back to the logBloom in our transaction receipt. This is the bloom filter for a specific transaction. Remember a transaction can have multiple logs so this represents the addresses/topics of all those logs.
0x00000000000000000000000000000000000000000000000000000000002000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000008000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000010800000000000000000000000000000000000000000000000000000000000000000100000000000000000000008000080000000000000000000000000000000000000000000002002000000000000000000000000004000000000000000000000000000000000000000000000000000800000000000000000000000000000000000000000If we refer back to our block header we have another logsBloom. This is the bloom filter for all transactions within the block. This is all the addresses/topics in every log of every transaction.
0x0100000000000004000000000000100000000000000000000000000000200000000000000000000000000000000001000000000000000000080008000000000040000000002000000000040800000000000000000000200000000000004800000040000002000000000000000000081000000000000040000000001080020000200001000000000000000000040000004000000000000000000000000010000000008000000000000800008000000800000000008000000200000800000000000000200a000000200000000000100002004000000000000000000000000020000000000080000020000000800000000000004000000000000000080000004000These bloom filters are represented in hex rather than binary. They are 256 bytes in length which represents a 2048-bit vector.
If we refer to the Llimllib example above our bit vector was 15 in length with bit index 2 and 13 flipped. If we convert that to hex let’s see what we get.
001000000000010 = 0x1002So while the hex may not look like a bit vector remember that it is under the hood.
Queries
If we remember our earlier query where we asked “get me all event logs of type Transfer with a “from” address of 0x5041ed759dd4afc3a72b8192c143f72f4724081a between blocks X & Y”.
We can take the Event signature topic, which represents the type Transfer along with the from value topic (0x5041ed759dd4afc3a72b8192c143f72f4724081a) and determine which bit indexes in the bloom filter should be set to 1.
If we use the logsBloom in the block header we can check if any of these bits aren’t set to 1. If they aren’t we can know with certainty that there are no logs that match that criteria in the block.
If we find the bits are set we know that a matching log may be in the block. We don’t know with certainty because the block header logsBloom is made up of multiple addresses and topics. It’s possible other event logs have set the matching bits. This is why a bloom filter is a probabilistic data structure.
The bigger the bit vector the less chance of a bit index collision from other logs.
Once we have a matching bloom filter we can query the individual receipt logsBloom using the same methodology. When we get a match we can view the actual log entries to retrieve the object.
By doing this from block X to Y we can quickly find & retrieve all logs that match our criteria.
That’s conceptually how the bloom filter works. Let’s now see the actual implementation used in Ethereum.
Geth Implementation - Bloom Filters
We understand how a bloom filter works but we want to know the exact steps of how we go from the address/topics to the logsBloom and see it done with a real block.
Ok no problem, we can start with the definition in the yellow paper. Don’t worry if it makes no sense right now we’re about to break it down.
The easiest way to show you what this means is to provide an example and reference back to the Geth client implementation.
Here’s the transaction log we looked at above on Etherscan.
We’re going to look at the first topic which is the Event signature 0xddf252ad1be2c89b69c2b068fc378daa952ba7f163c4a11628f55a4df523b3ef and show how this value is converted into which bit indexes should be updated.
Below is the bloomValues function from the Geth codebase. This is the function takes in data such as the Event signature topic 0xddf252ad1be2c89b69c2b068fc378daa952ba7f163c4a11628f55a4df523b3ef and give us back the bit indexes that need to be updated in the bloom filter. Let’s run through it.

The function takes in the data ie a topic (In our case the event signature topic) and a hashbuf which is just an empty byte array of length 6.
Refer back to the yellow paper snippet, “the first three pairs of bytes in a Keccak-256 hash of the byte sequence”. Three pairs of bytes are equal to 6 bytes which is why our hashbuf is of length 6.
The data for our example is 0xddf252ad1be2c89b69c2b068fc378daa952ba7f163c4a11628f55a4df523b3ef
The sha commands between lines 140 - 144 hashes the data input and load the output into the hashbuf.
The sha output, which uses keccak256, is ada389e1fc24a8587c776340efb91b36e675792ab631816100d55df0b5cf3cbc.
You can verify this using the online keccak 256. (Note make sure you change the input type from text to hex. When using keccak 256 for function signatures the input is of type text whereas here it is of type hex.)
The hasbuf now has contents [ad, a3, 89, e1, fc, 24] (in hex). Remember each hexadecimal character represents 4 bits so 2 characters represent an 8-bit byte.
v1 is calculated.
hashbuf [1] = 0xa3 = 10100011 is used with a bitwise AND against 0x7. 0x7 = 00000111 in binary.
A byte is composed of 8 bits, if we want to obtain a bit index we need to ensure the value we get is between 0 and 7 for a zero index array. Using a bitwise AND constrains hashbuf [1] to be a value between 0 and 7. In our case, it is a 3 = 00000011.
This bit index value is used with a bit shift operator to create an 8-bit byte with the flipped bit at the correct index, 00001000.
v1 is the whole byte rather than the actual bit index because this value will later be used with a bitwise OR on the bloom filter. The OR will ensure all corresponding bits in the bloom filter will also be flipped.
We now have the byte value but we still need the byte index. Our bloom filter is 256 bytes (2048 bits) in length so we need to know which byte to run the bitwise OR on. The value i1 represents this byte index.
Note we use a big-endian uint16 with our hashbuf, this will constrain it to the first 2 bytes of the array. In our case this represents 0xada3 = 1010110110100011.
We use this value with a bitwise AND against 0x7ff = 0000011111111111. If you count the number of bits set to 1 in 0x7ff you’ll notice there are eleven. From the yellow paper, “It does this through taking the low-order 11 bits of each of the first three pairs”. This yields us the value 0000010110100011.
This value is then bit shifted down by 3. This turns an 11-bit number into an 8-bit number. We want a byte index and our bloom filter has a byte length of 256 so we need our byte index value to be in that range. An 8-bit number can be any value from 0 to 255. In our case, this value is 180.
We calculate our byte index bus using the BloomByteLength which we know is 256 minus our calculated value 180, minus 1. The minus 1 is to keep the result between 0 to 255. This gives us our byte index to update, in this case it’s byte 75.
This is telling us to update the bit index 3 (0 index so 4th bit) in the 75th byte of the bloom filter. This can be done by running a bitwise OR of v1 against the 75th byte in the bloom filter.
Note we’ve only covered the first “byte pair” 0xada3, This is done again for “byte pair” 2 and 3. Each address/topic will update 3 bits in the 2048-bit vector. From the yellow paper, “specialised Bloom filter that sets three bits out of 2048”.
“Byte pair” 2 states update bit index 1 in byte 195
“Byte pair” 3 states update bit index 4 in byte 123
If the bit to be changed has already been flipped by another topic it will stay as is otherwise it will be flipped to a 1.
So in conclusion we have determined that the Event signature topic will flip the following bits in the bloom filter.
bit index 3 in byte 75
bit index 1 in byte 195
bit index 4 in byte 123
Take a look at the logBlooms in the transaction receipt convert it to binary and you can verify those bit indexes are set.
I’ve compiled this example into a Github repo evm-by-example for you to play around with. Check out the bloom folder it will definitely help consolidate what you’ve learned in the article.
For those interested in going a little deeper down the rabbit hole have a look at the BloomBits Trie.
Till next time.
noxx
Twitter @noxx3xxon






Thanks for sharing the topic, which introduces the EVM mechanism step by step. I think it isn't easy to understand the EVM before reading your series deeply. Now, that's changed and inspired me more curiosity. Thanks for your sharing.
This is one of the best series I have ever read. Thank you and please keep writing :)